Итак смысл игры: игрок называет число в чем то и пишет, во что его надо перевести. Далее другие игроки, пользуясь знаниями и калькулятором переводят его в указанёную величину. Можно давать промежуточные ответы. Кто первым назовет верное число, загадывает следующее и пишет во что перевести. Можно давать задание любой сложности. Но чтоб не было задания секунды переводить в килограммы :3
Пример:
1 игрок: 2 дня перевести в часы.
2 игрок: 48 часов
2 игрок: 3 тонны перевести в граммы
3 игрок:...
Итак, я начну.
9 месяцев, перевести в секунды.
Сообщений: 38
Страница 1 из 1
Страница 1 из 1
Переведи в...
Ай, мой Пинки-калькулятор заклинило и мне не хорошо!
А можно месяц за 30 дней принимать?
23328000сек
Задача: перевести 20 из восьмеричной системы в шестнадцатеричную.
Задача: перевести 20 из восьмеричной системы в шестнадцатеричную.
10.
Перевести 59 из десятичной системы в единичную. Муахахаха.
Перевести 59 из десятичной системы в единичную. Муахахаха.
Эээ... 5,9, округляем до 6? *жестко тупит*
11111111111111111111111111111111111111111111111111111111111
изи
изи
Задача: перевести 345 Эргов в Джоули
А вот теперь моя очередь тупить. Что есть эрг?
SMT5015 писал(а):А вот теперь моя очередь тупить. Что есть эрг?
единица измерения энергии в СГС
0,000034
Переведите мне пять лет в наносекунды.
Переведите мне пять лет в наносекунды.
15768*10^13 наносекунд
Ну пусть будет 50дин*см^-2 в Паскали.(вики в помощь)
Окей, я без понятия, что это, но у меня вышло в ответе 5
Ладно, немного попонятнее: рассчитайте отношение времени существования Вселеной, согласно теории Большого Взрыва, по современным данным, с округлением значения до десятых, к средней продолжительности жизни мужчиского населения России по наиболее современной статистике, с округлением до до целого числа лет. Результат округлить до сотых долей при приведении к виду записи числа в СИ.
Ладно, немного попонятнее: рассчитайте отношение времени существования Вселеной, согласно теории Большого Взрыва, по современным данным, с округлением значения до десятых, к средней продолжительности жизни мужчиского населения России по наиболее современной статистике, с округлением до до целого числа лет. Результат округлить до сотых долей при приведении к виду записи числа в СИ.
Я ввел эти значения в калькулятор, и в ответ он мне показал счастливую рожицу...
SteamBrony писал(а):Окей, я без понятия, что это, но у меня вышло в ответе 5
Ладно, немного попонятнее: рассчитайте отношение времени существования Вселеной, согласно теории Большого Взрыва, по современным данным, с округлением значения до десятых, к средней продолжительности жизни мужчиского населения России по наиболее современной статистике, с округлением до до целого числа лет. Результат округлить до сотых долей при приведении к виду записи числа в СИ.
а погрешность рассчитать?
Не, можно без неё.
215593750,00 (про округление немного некорректно сказано, ну да ладно)
Нафиг перевод величин, держите задачку:
Самолёт (реактивный или винтовой) стоит на взлётной полосе с подвижным покрытием (типа транспортёра). Покрытие может двигаться против направления взлета самолёта. Оно имеет систему управления, которая отслеживает и подстраивает скорость движения полотна таким образом, чтобы скорость вращения колёс самолёта была равна скорости движения полотна. Вопрос: сможет ли самолёт взлететь в таких условиях?
Нафиг перевод величин, держите задачку:
Самолёт (реактивный или винтовой) стоит на взлётной полосе с подвижным покрытием (типа транспортёра). Покрытие может двигаться против направления взлета самолёта. Оно имеет систему управления, которая отслеживает и подстраивает скорость движения полотна таким образом, чтобы скорость вращения колёс самолёта была равна скорости движения полотна. Вопрос: сможет ли самолёт взлететь в таких условиях?
Нет. Самолет ежет по полотну , которое движется в обратную сторону с такой же скоростью, то есть он стоит на месте. Е взлетит, хотя если будет ураган....
Ок я пропускаю ход давайте кто умный за меня придумайте задачу...
Stitch писал(а):Нет. Самолет ежет по полотну , которое движется в обратную сторону с такой же скоростью, то есть он стоит на месте. Е взлетит, хотя если будет ураган....
Я не сказал, что ты решил правильно) по крайней мере надо объяснить свою точку зрения. Может у кого есть другое мнение?
Задача некоректна. Может, не стоит?
SteamBrony писал(а):Задача некоректна. Может, не стоит?
Истинно так. Не стоит, а взлетает.)
SteamBrony писал(а):Задача некоректна. Может, не стоит?
Окей, но по-моему не взлетит) Получается что если полотно движется с точно такой же скоростью как и самолет, то он будет неподвижен относительно земли-> подъемной силы не возникнет. Единственное, что он может сдвинуться относительно полотна, если сила реактивной тяги превысит силу трения. Но это не будет полет.
VIM писал(а):SteamBrony писал(а):Задача некоректна. Может, не стоит?
Истинно так. Не стоит, а взлетает.)
в самом начале стоит, потом начинает взлетать
Я имел в виду, что данное обсуждение этого не стоит продолжать ввиду того, что данная дискуссия может быть неограниченно долгой из-за некоректности поставленных условий. Т.е. при данных обстоятельствах, обе точки зрения могут являтся верными. Особенно, при учёте известности данной задачи в сети и наличии десятков различных объяснений.
Ладно, я создал тему, значит я выбираю. SteamBrony, ты понял, что задача некорректна , ты задаешь следующую)
Что? Я? Ну ладно... У меня есть одна, которую я, вроде как, придумал сам (хоть она и использует принцип одной каверзной задачки и, фактически, некоторое переосмысленые целого цикла подобных, и я не уверен, что её до этого не существовало, но ладно, будем считать, что я проявил немного креативности)
Вот сама задачка (математики тут особой нет, только логика и смекалка, поэтому высчитывать различные погрешности не надо) :
У вас есть две кружки, без миллилировых делений, но вы точно знаете их ёмкость - 250 и 300 мл. Или даже скорее банки цилиндрической формы (но самих параметров, вроде высоты, диаметра основания, толщины стенок, вы не знаете, только объём). Также, на всякий случай, есть ещё одна свободная ёмкость, но с неизвестным, но значительным объёмом, и более сложной формы (усечённый конус, к примеру). И источник воды, к примеру, водопроводный кран (при этом скорость течения воды в нём димамично меняется и такова, что кружка наполняется практически тут же). Самими кружками можно манипулировать достаточно свободно (но из-за наличия ручек, нельзя вставить одну кружку в другую) - можно переливать воду из одной кружки в другую (при этом можно не выливать до конца), можно в свободную тару (можно и обратно), сами кружки при переливании можно ставить на бок под любым углом (я бы сделал условие НАМНОГО меньше, но это - предотвращение лишних вопросов от тех, кто захочет решить задачу, используя, к примеру, закон Архимеда или секундомер (которого нет) и кран :) (ну а вдруг) - не стоит усложнять ситуацию там, где не надо) .
Вообщем, суть задачи такова - используя только кран, обе кружки, и свободную ёмкость (которая может и не использоваться, при желании). получить в одной из кружек ровно (будем считать, что у вас твёрдая рука и хорошая реакция, и переливания нет) 75 мл воды. Подсказка - чтобы решить эту задачу, нужно понять, как можно наполнить обе кружки (и необязательно одновременно) с известным объёмом ровно наполовину. Привести решение в виде операций, желательно, с пояснением.
Вот сама задачка (математики тут особой нет, только логика и смекалка, поэтому высчитывать различные погрешности не надо) :
У вас есть две кружки, без миллилировых делений, но вы точно знаете их ёмкость - 250 и 300 мл. Или даже скорее банки цилиндрической формы (но самих параметров, вроде высоты, диаметра основания, толщины стенок, вы не знаете, только объём). Также, на всякий случай, есть ещё одна свободная ёмкость, но с неизвестным, но значительным объёмом, и более сложной формы (усечённый конус, к примеру). И источник воды, к примеру, водопроводный кран (при этом скорость течения воды в нём димамично меняется и такова, что кружка наполняется практически тут же). Самими кружками можно манипулировать достаточно свободно (но из-за наличия ручек, нельзя вставить одну кружку в другую) - можно переливать воду из одной кружки в другую (при этом можно не выливать до конца), можно в свободную тару (можно и обратно), сами кружки при переливании можно ставить на бок под любым углом (я бы сделал условие НАМНОГО меньше, но это - предотвращение лишних вопросов от тех, кто захочет решить задачу, используя, к примеру, закон Архимеда или секундомер (которого нет) и кран :) (ну а вдруг) - не стоит усложнять ситуацию там, где не надо) .
Вообщем, суть задачи такова - используя только кран, обе кружки, и свободную ёмкость (которая может и не использоваться, при желании). получить в одной из кружек ровно (будем считать, что у вас твёрдая рука и хорошая реакция, и переливания нет) 75 мл воды. Подсказка - чтобы решить эту задачу, нужно понять, как можно наполнить обе кружки (и необязательно одновременно) с известным объёмом ровно наполовину. Привести решение в виде операций, желательно, с пояснением.
Наличие твердой руки и хорошей реакции дает какие-то возможности? Например, на глазок налить емкость ровно наполовину.
Рискну предположить, что иначе задача не решается, т.к. мы не сможем получить объем не кратный 50.
Рискну предположить, что иначе задача не решается, т.к. мы не сможем получить объем не кратный 50.
Эта задачка очень напомнила мне то испытание у фонтана из "Крепкого орешка 3" :)
strikeX100 писал(а):Наличие твердой руки и хорошей реакции дает какие-то возможности? Например, на глазок налить емкость ровно наполовину.
Рискну предположить, что иначе задача не решается, т.к. мы не сможем получить объем не кратный 50.
Нет, уверяю вас, она решаема, и без "на глазок") Я специально выделил важные слова жирным шрифтом, чтобы дать вам подсказку и вы сразу не сдавались:
SteamBrony писал(а):Или даже скорее банки цилиндрической формы
Этого факта вполне достаточно.
SteamBrony писал(а):SteamBrony писал(а):Или даже скорее банки цилиндрической формы
Этого факта вполне достаточно.
Т.е. отмерив 50 мл, допустимо "на глазок" вылить половину этого объёма и таким образом получить 25 мл?
Окей
Полностью наполним кружку емкостью 250мл. Потом поставим её так как указано на рисунке:
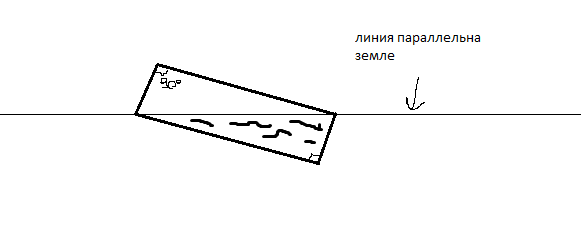
Из нее вытечет ровно половина воды и останется 125мл. Переливаем 125мл в большую емкость, наполняем 250 миллилитровую емкость и переливаем воду из нее в 300 миллилитровую. Доливаем воду из большой емкости в 300 миллилитровую и в ней(большой емкости) останется 75 мл.
Полностью наполним кружку емкостью 250мл. Потом поставим её так как указано на рисунке:

Из нее вытечет ровно половина воды и останется 125мл. Переливаем 125мл в большую емкость, наполняем 250 миллилитровую емкость и переливаем воду из нее в 300 миллилитровую. Доливаем воду из большой емкости в 300 миллилитровую и в ней(большой емкости) останется 75 мл.
Да, именно это - правильное решение. Ход операций может быть другим, но по сути, всё приходит к одному результату.
Тогда такая задача.
Дано: неограниченно большой лист бумаги толщиной 0.1мм
Вопрос: сколько раз необходимо согнуть пополам, делая каждый из сгибов перпендикулярно предыдущему, чтобы получившаяся бумажная фигура достала до Луны(которая планета, а не принцесса)?
Дано: неограниченно большой лист бумаги толщиной 0.1мм
Вопрос: сколько раз необходимо согнуть пополам, делая каждый из сгибов перпендикулярно предыдущему, чтобы получившаяся бумажная фигура достала до Луны(которая планета, а не принцесса)?
strikeX100 писал(а):Тогда такая задача.
Дано: неограниченно большой лист бумаги толщиной 0.1мм
Вопрос: сколько раз необходимо согнуть пополам, делая каждый из сгибов перпендикулярно предыдущему, чтобы получившаяся бумажная фигура достала до Луны(которая планета, а не принцесса)?
Не планета, а спутник Земли. А кто гнуть-то будет?))) "Разрушители легенд" на десятом сложении спеклись, ЕМНИП.
1) да, спутник, ошибся.
2) техническими проблемами складывания можно не заморачиваться.
2) техническими проблемами складывания можно не заморачиваться.
strikeX100 писал(а):1) да, спутник, ошибся.
2) техническими проблемами складывания можно не заморачиваться.
Что-то там про 2 в степени n-1 и т.д. Умаешься считать. Но пухлость получающейся бумажной "вавилонской башни", полагаю, тоже не будет учитываться? Ну и ладно.)
Сообщений: 38
Страница 1 из 1
Страница 1 из 1